Куда исчезает неопределенность в энергии при ее измерении?

 

В.Л. Янчилин

 

(Получена 4 октября 2007; опубликована 15 октября 2007)

 

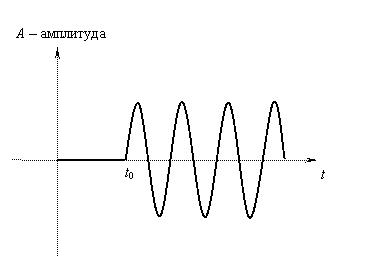
Показано, что при выполнении законов сохранения в микромире, ключевую роль играют нелокальные связи.

 

 

1. Постановка проблемы

 

Рассмотрим атом, который переходит из возбужденного состояния в основное, излучая при этом фотон. Время Dt, в течение которого атом излучает фотон, конечно, и поэтому фотон обладает неопределенностью в энергии: De×Dt ³ ħ/2. Это можно прокомментировать так. Фотон, обладающий строго определенной энергией e, должен также обладать строго определённой частотой w = e/ħ. Но строго определённой частотой может обладать только бесконечный во времени периодический процесс. Если же процесс имеет начало во времени, то сам переход от нулевой частоты к некоторой определенной частоте уже не будет обладать определённой частотой (см. рис. 1).

Рис. 1. Строго периодический процесс не обладает какой-либо определенной частотой в момент своего начала, вблизи точки t₀.

 

Следовательно, фотон в момент своего рождения не может обладать определённой частотой, а, значит, и определённой энергией. Но, родившись с неопределённой энергией, фотон будет в дальнейшем сохранять эту неопределённость в силу закона сохранения энергии. Соответственно, будет сохраняться и неопределённость в его частоте. Пусть наиболее вероятное значение энергии фотона равно e₀ (см. рис. 2).

При регистрации фотона классическим прибором фотон исчезает, а его энергия передается прибору. Если время регистрации фотона не ограничено, то переданная им энергия может быть измерена с какой угодно точностью. И здесь возникает интересный парадокс.

Фотон, обладающий неопределенной энергией, передает классическому прибору вполне определенную энергию. Куда же исчезает неопределенность в энергии фотона?

При регистрации фотона энергия классического прибора может возрасти на любую величину e из интервала (e₀ - De, e₀ + De). Допустим, она возросла на величину e₁ < e₀. В этом случае энергия, переданная прибору, будет меньше, чем средняя энергия фотона. Куда в таком случае исчезает недостающая энергия? Но существует также вероятность, что энергия прибора возрастет на величину e₂ > e₀. В этом случае энергия, переданная прибору, будет больше, чем средняя энергия фотона. Откуда взялся этот излишек энергии?

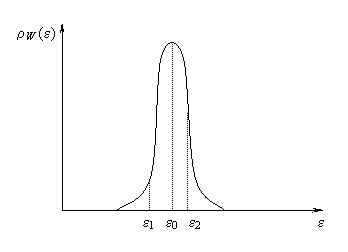
Рис. 2. Фотон обладает непрерывным набором энергий вблизи некоторого среднего значения e₀. Вероятность обнаружить у фотона энергию e пропорциональна r_W (e).

 

Подобные вопросы возникают при измерении любых сохраняющихся величин. Например, электрон, обладающий неопределенным импульсом, передает классическому прибору вполне определенный импульс, который может быть несколько больше или несколько меньше среднего импульса электрона. Как же в таком случае быть с законом сохранения импульса?

 

 

2. Принцип локальности или принцип неопределенности?

 

Эти проблемы встали со всей остротой уже на заре создания квантовой механики. Довольно интересное решение предложил Нильс Бор (совместно с Г. Крамерсом и Дж. Слетером) в статье «Квантовая теория излучения», опубликованной в 1924 году. Бор предположил, что в микромире законы сохранения выполняются не строго, а лишь статистически. В каждом отдельно взятом элементарном процессе баланс энергии незначительно нарушается либо в сторону избытка энергии, либо, наоборот, – ее недостатка. Но, тем не менее, если мы рассмотрим большое число элементарных процессов, то в среднем энергия будет сохраняться.

 

В случае перехода под действием собственного виртуального излучения мы будем предполагать, что изменение импульса распределено согласно вероятностному закону таким образом, что изменения импульса, обусловленные переходами в различных атомах, статистически компенсируются для любого направления в пространстве.

Причину наблюдаемого статистического сохранения энергии и импульса мы будем искать не в каком-либо отклонении от электродинамической теории света при распространении излучения в пустом пространстве, а в особенностях взаимодействия между виртуальным полем излучения и облучаемыми атомами [1,с.533].

 

А вот что за год до этого писал Бор о сохранении момента импульса:

 

при объяснении спектров следует принимать такие требования для процессов поглощения, при которых не может быть и речи о простом сохранении момента импульса [2,с.525].

 

Однако последующие, более точные, эксперименты, проведенные Артуром Комптоном и другими физиками, показали, что законы сохранения энергии и импульса строго выполняются в каждом отдельно взятом элементарном процессе.

 

И здесь возникает очень интересная проблема, потому что невозможно согласовать между собой следующие три утверждения.

Первое утверждение. Законы сохранения (импульса, энергии, момента импульса) строго выполняются в каждом отдельно взятом элементарном процессе.

Второе утверждение. В движении квантовых объектов существует неопределенность.

Третье утверждение. В микромире выполняется принцип локальности.

 

Первое утверждение понятно без комментариев, два другие имеет смысл пояснить во избежание недоразумений.

Неопределенность в движении квантовых объектов означает, что, например, электрон (как и любой другой квантовый объект) может в одно и то же время находиться в разных местах пространства и обладать различными значениями импульса и энергии. Хотя такое утверждение выглядит, мягко говоря, странным (а для тех, кто впервые сталкивается с квантовой механикой – просто абсурдным), оно непосредственно вытекает из основного принципа квантовой механики – принципа суперпозиции. Действительно, если электрон может находиться в области А (обозначим такое состояние как Y_А) и может находиться в области В (обозначим такое состояние как Y_В), то он может также находиться в состоянии Y_АВ:

 

Y_АВ = aY_А + bY_В,

 

где a, b – произвольные комплексные числа, нормированные условием |a|² + |b|² = 1. В этом случае электрон будет находиться одновременно и в области А (вероятность зарегистрировать его там равна |a|²) и в области В (вероятность |b|²).

 

Чтобы убедится, что электрон действительно находится сразу в двух областях, достаточно привести их во взаимодействие между собой и наблюдать различные интерференционные эффекты, которых не было бы, если бы электрон находился только в одной области. Кто-то, возможно, захочет возразить, что для наблюдения интерференционных явлений необходимо большое число частиц, и поэтому здесь все не так очевидно. Это не верно. Для получения интерференционной картины, действительно, нужно иметь много частиц, но интерференцию можно наблюдать при помощи всего одной частицы. Уровень современной техники уже позволяет проводить подобные эксперименты (см., например [3]).

 

Соответственно, если электрон может находиться в состоянии с определенным импульсом р₁ (обозначим как Y₁) и в состоянии Y₂ с определенным импульсом р₂, то он также может находиться в состоянии Y₁₂:

 

Y₁₂ = aY₁ + bY₂.

 

Более того, в соответствии с соотношением неопределенностей Гейзенберга, электрон не может находиться в состоянии с определенным импульсом и при этом занимать определенное положение в пространстве. Действительно, определенный импульс подразумевает определенное волновое число. А определенное волновое число подразумевает бесконечный в пространстве строго периодический процесс.

 

Теперь перейдем к принципу локальности, который утверждает, что воздействие одного объекта на другой передается с конечной скоростью (не превышающей скорость света в вакууме). Кроме того, это воздействие передается посредством материального носителя – поля, которое обладает импульсом и энергией и перемещается от одного объекта к другому, последовательно проходя все точки разделяющего их пространства. Согласно классической физике, включающей в себя также и теорию относительности, принцип локальности всегда строго выполняется без каких-либо ограничений.

 

Однако нетрудно показать, что три перечисленных выше утверждения не могут быть одновременно истинными в микромире. Каким-то из них необходимо пожертвовать. Но каким?

 

 

3. Позиция Эйнштейна

 

Как уже отмечалось выше, первоначально, Нильс Бор попытался частично пожертвовать законами сохранения и оказался неправ. Тем не менее, позиция Бора достойна восхищения, ибо уже тогда он понимал, что принципом неопределенности жертвовать нельзя. Принцип неопределенности – это фундамент квантовой механики, это то новое, что квантовая механика внесла в физику. И Бор ясно понимал, что без этого принципа невозможно описать странное поведение субатомных частиц.

 

Несколько иную позицию в этом вопросе занял Эйнштейн. Он был согласен с тем, что в квантовой механике, основанной на принципе неопределенности, есть рациональное зерно. Однако он безоговорочно верил и в законы сохранения и в принцип локальности, и именно поэтому отверг принцип неопределенности, сделав отсюда вывод о неполноте квантовой механики. Несомненная заслуга Эйнштейна в том, что он смог просто и ясно показать несовместимость трех перечисленных утверждений в физике микромира. Рассмотрим аргументы Эйнштейна.

 

Предположим, две частицы некоторое время взаимодействуют друг с другом, а затем разлетаются в разные стороны. Согласно квантовой механике каждая частица обладает и неопределенностью в местоположении и неопределенностью в импульсе. Однако Эйнштейн обратил внимание на следующую деталь. Мы можем сколь угодно точно измерить импульс первой частицы и затем, основываясь на законе сохранения импульса, определить импульс второй частицы. И, кроме того, мы можем сколь угодно точно измерить местоположение первой частицы и затем, исходя из того, что центр масс замкнутой системы всегда остается строго на одном месте (предполагается, что движение частиц описывается в системе отсчета, где их центр масс изначально покоился), определить местоположение второй частицы.

 

А теперь простой вопрос. Может ли измерение, проделанное над первой частицей, изменить состояние второй частицы, которая в общем случае находится сколь угодно далеко от первой?

Человек, недостаточно хорошо знакомый с квантовой механикой, скорее всего, поспешит отрицательно ответить на этот вопрос. Но мы торопиться не будем и внимательно рассмотрим оба варианта ответа.

 

Первый вариант. Если мы предполагаем, что принцип локальности строго выполняется в микромире, то тогда мы вынуждены сделать следующий вывод. Измерение импульса первой частицы не могло повлиять на физическое состояние второй частицы, и, следовательно, вторая частица обладала определенным импульсом уже до того, как мы измерили импульс первой. Измерение координаты первой частицы также не могло повлиять на физическое состояние второй частицы и, следовательно, вторая частица находилась в определенном месте пространства уже до того, как мы определили местоположение первой. Таким образом, вторая частица сразу же после взаимодействия с первой частицей обладала определенным импульсом и имела в каждый момент времени определенное местоположение в пространстве. Исходя из этого, можно сделать вывод, что соотношение неопределенностей Гейзенберга отражает не реальное состояние частицы, а лишь наше незнание этого состояния. И в этом смысле квантовая механика не дает полного описания происходящих в микромире процессов. Именно этот вывод и сделал Эйнштейн в своей знаменитой статье «Можно ли считать квантовомеханическое описание физической реальности полным?», написанной совместно с Н. Розеном и Б. Подольским в 1935 году [4].

 

Второй вариант. Если мы предполагаем, что неопределенность в местоположении и импульсе частицы существует реально (а есть масса экспериментов, подтверждающих это) и, кроме того, предполагаем строгое выполнение законов сохранения импульса и энергии в каждом элементарном процессе, то мы вынуждены сделать следующий вывод. Принцип локальности в микромире неприменим. А именно: измерение, проделанное над первой частицей, может изменить реальное состояние (а не только наше знание об этом состояние) второй частицы, находящейся сколь угодно далеко от первой.

 

Итак, если, изменяя состояние одной частицы, мы не можем повлиять на физическое состояние другой частицы, то принцип неопределенности не верен. И наоборот, если принцип неопределенности верен, то, измеряя, скажем, импульс одной частицы мы тут же изменяем физическое состояние второй частицы. Это очень хорошо понимал уже Эйнштейн, и только поэтому он отвергал принцип неопределенности. Это также понимали и Эрвин Шредингер и Луи де Бройль. Вот что писал Луи де Бройль:

 

Высказываясь о своей статье, написанной совместно с Подольским и Розеном, Эйнштейн заметил, что аргументация Бора очень ясна. Она сводит все к выбору между двумя следующими утверждениями:

1. Описание системы с помощью волновой функции y  является полным.

2. Истинные состояния двух пространственно разделенных объектов независимы друг от друга.

Точка зрения Бора состоит в том, что принимается утверждение 1, а утверждение 2 отвергается.

Что же касается Эйнштейна, то он предпочитает принять постулат 2 и рассматривать волну y  лишь как статистическую характеристику ансамбля систем, находящихся в одном и том же состоянии.

Как мне кажется, точка зрения Эйнштейна допускает то возражение, что определение пространственной разделенности двух систем нельзя считать простым, поскольку локализация этих систем неполная и области локализации двух систем в пространстве могут перекрываться. Впрочем, этот тонкий вопрос требует дальнейшего изучения.

Мы видим, насколько тонким оказываются вопросы интерпретации современной квантовой теории. Самые крупные ученые нашего времени полностью расходились во мнениях по этому вопросу [5].

 

Луи де Бройль чувствовал себя очень неуютно в мире, где нарушается принцип локальности. И спустя почти четверть века он предпринял попытку отойти от ортодоксальной квантовой механики [6]. Что касается Эрвина Шредингера, то, полностью доверяя принципу локальности, он стал даже отрицать реальность квантовых скачков в своей нашумевшей статье «Существуют ли квантовые скачки?» [7].

 

К сожалению, бóльшая часть из последующего поколения физиков уже не достаточно ясно осознавала тот факт, что принцип локальности несовместим с принципом неопределенности (в законах сохранения уже никто не сомневался). И многие физики одновременно верили и в полноту квантовой механики, и в принцип локальности, не понимая, что одно противоречит другому (см., например, [8-10]).

 

В настоящее время нелокальный характер квантовой механики – это многократно проверенный экспериментальный факт (не говоря уже о принципе неопределенности). Причем, бóльшая часть экспериментов по обнаружению нелокальных связей первоначально проводилась физиками, не верящими в саму возможность такого взаимодействия. Они хотели своими экспериментами доказать, что никакой нелокальности в микромире не существует, но доказали как раз обратное!

 

А какие аргументы против нелокальности выдвигали физики, не желавшие ее принимать?

Читая статьи Эйнштейна [4,11-14] становится ясно, что он отвергал нелокальность по принципу «этого не может быть, потому что этого не может быть никогда». Как только Эйнштейн доходил до возможности нелокального взаимодействия, он тут же поворачивал обратно, словно бы говоря: «Ну вот, видите, мы пришли к противоречию, дальше идти нельзя». В своем неприятии нелокальности Эйнштейн ссылался на свою интуицию. Интуиция Эйнштейна вещь, безусловно, весьма ценная и к ней стоит прислушаться, но в данном случае это не аргумент. Эрвин Шредингер также не выдвигал никаких аргументов против нелокальности, а просто обзывал ее магией. Луи де Бройль соглашался с ним [15]. Возражения менее значимых физиков против нелокальности мы приводить не будем.

 

Таким образом, выясняется, что единственной причиной, мешающей многим физикам принять нелокальность, является их предубеждением против этого явления. Других причин просто нет!

 

 

4. Ключевая роль нелокальных связей

 

После такого длинного отступления вернемся к законом сохранения и посмотрим, как именно они выполняются в микромире на простом примере излучения атомом фотона. Учитывая все вышесказанное, мы можем сделать следующий вывод. Между атомом и испущенным им фотоном существует нелокальная связь. Неопределенность в движении фотона и неопределенность в движении атома неразрывно связаны между собой. Эта связь никак не зависит от расстояния и нисколько не ослабевает по мере удаления фотона от атома. Ее суть в том, что измерение, проделанное над фотоном, мгновенно изменяет состояние атома и наоборот. Допустим, мы хотим измерить импульс фотона с очень высокой точностью. До измерения фотон обладал непрерывным набором импульсов в некотором интервале вблизи среднего значения. Атом, испытавший отдачу, после испускания фотона также обладал непрерывным набором импульсов. Но как только мы измеряем импульс фотона (чтобы это сделать нужно каким-то образом «вынудить» фотон принять определенный импульс) атом, несмотря на то, что может находиться сколь угодно далеко от фотона, также приобретает определенный импульс. Чем точнее мы измеряем импульс одной частицы, тем более точный импульс приобретает другая. Конечно, при условии, что изначально вся система обладала определенным импульсом. А если система, в данном случае возбужденный атом, не обладала определенным импульсом? В этом случае должна существовать нелокальная связь между этим атомом и каким-то другим объектом. Например, объектом, который взаимодействовал с возбужденным атомом, прежде чем тот испустил фотон.

 

Когда мы измеряем импульс атома, фотон также приобретает определенный импульс. При этом нелокальная связь между ними безвозвратно теряется. После этого и атом и фотон могут быть описаны при помощи разных волновых функций. Состояние атома описывается своей волновой функцией, которая зависит только от его координат, а состояние фотона – своей. Такое описание было невозможным, пока между ними существовала нелокальная связь. Так как в этом случае вероятность обнаружить атом в какой-либо точке пространства зависела помимо всего прочего и от состояния фотона. И наоборот. Система атом-фотон представляла собой единое целое и описывалась одной волновой функцией, зависящей как от местоположения атома, так и от местоположения фотона. И эту волновую функцию было невозможно разделить на две: свою для атома и свою для фотона. Возможно, именно поэтому в современной квантовой механике часто используется термин «запутанного квантового состояния», аналогичный термину «нелокальная связь».

 

В качестве иллюстрации сказанного рассмотрим следующий эксперимент, описание которого взято из [16]:

 

T. Wilk и ее коллеги из Германии и Великобритании разработали методику получения запутанных (entangled) квантовых состояний двух фотонов посредством единичного атома. В оптическую ловушку захватывался атом рубидия. Под влиянием короткого лазерного импульса атом излучал фотон, в результате чего атом и испущенный фотон становились «запутанными». Примерно через микросекунду следующий импульс лазера вызывал испускание атомом второго фотона, который оказывался в запутанном состоянии с первым фотоном. Таким образом, квантовое состояние переходило с атома на второй фотон, и возникала пара фотонов в запутанном состоянии.

 

Итак, атом испускает фотон, продолжая оставаться с ним в нелокальной связи. Затем он испускает второй фотон, оставаясь с ним также в нелокальной связи. При этом вся система, состоящая из атома и двух фотонов, представляет собой единое целое. Измерения, проделанные над одним фотоном, мгновенно влияют не только на состояние атома, но и на состояние другого фотона.

 

Литература

 

1.             Бор Н., Крамерс Г., Слетер Дж. Квантовая теория излучения // Бор Н. Избранные научные труды в 2-х т. М.: Наука, 1970, т.1, с.526-541.

2.             Бор Н. О применении квантовой теории к строению атома. I. Основные постулаты квантовой теории // Бор Н. Избранные научные труды в 2-х т. М.: Наука, 1970, т.1, с.482-525.

3.             Дойч Д., Экерт А. Введение в квантовые вычисления // Физика квантовой информации. М.: Постмаркет, 2002, с.126-139.

4.             Эйнштейн А., Подольский. Н., Розен Б. Можно ли считать квантовомеханическое описание физической реальности полным? // Эйнштейн А. Собрание научных трудов в 4-х т. М.: Наука, 1966, т.3, с.604-611.

5.             Де Бройль Л. Соотношения неопределенностей Гейзенберга и вероятностная интерпретация волновой механики. М.: Мир, 1986, с.192.

6.             Де Бройль Л. Останется ли квантовая физика индетерминистической? // Вопросы причинности в квантовой механике. М.: ИЛ, 1955, с.11-33.

7.             Шредингер Э. Существуют ли квантовые скачки? // Шредингер Э. Избранные труды по квантовой механике. М.: Наука, 1976, с.261-284.

8.             Мигдал А. Квантовая физика для больших и маленьких. М.: Наука, 1989, с.92,96.

9.             Пайерлс Р. Сюрпризы в теоретической физике. М.: Наука, 1988, с.38.

10.         Демуцкий В., Половин Р. Концептуальные вопросы квантовой механики // Успехи физических наук. 1992, т. 162, №10, с.130,136.

11.         Эйнштейн А. Замечание о квантовой теории // Эйнштейн А. Собрание научных трудов в 4-х т. М.: Наука, 1966, т.3, с.528-530.

12.         Эйнштейн А. Квантовая механика и действительность // Там же, с.612-616.

13.         Эйнштейн А. Элементарные соображения по поводу интерпретации основ квантовой механики // Там же, с.617-622.

14.         Эйнштейн А. Вводные замечания об основных понятиях // Там же, с.623-626.

15.         Де Бройль Л. Интерпретация волновой механики // Философские вопросы современной физики. М.: Государственное издательство политической литературы, 1958, с.95.

16.         Ерошенко Ю. Запутанные состояния фотонов // Новости физики в сети Internet. УФН т.177, №8, 2007.