Глава 4

Квантовые компьютеры. Практическая реализация

 

4.1. Квантовый процессор

 

Теперь, когда вы достаточно хорошо представляете себе, что такое кубиты, рассмотрим, каким же образом они реализуются в физических системах и, прежде всего, в качестве ячеек памяти (регистров) квантового компьютера. В этом разделе я сделаю краткий обзор научных публикаций, касающихся практической реализации квантового компьютера, и приведу мнение ученых насчет того, когда же можно ожидать его воплощения «в железе», и когда будет налажено его коммерческое производство.

Основные работы над аппаратным обеспечением (hardware) квантового компьютера продвигаются в следующих направлениях:

● создание квантового процессора;

● создание устройств для хранения квантовой информации (квантовая память);

● разработка квантовой шины для обмена информацией.

 

Сразу стоит отметить, что это лишь аналоги соответствующих устройств классического компьютера, которые будут существенно от них отличаться.

Наибольшие усилия и средства в настоящее время направлены на решение первого вопроса, и здесь достигнуты значительные успехи. При разработке квантового процессора необходимо, прежде всего, выбрать физическую систему, физическую основу процессора, которая бы отвечала следующим требованиям.

· Физическая система, представляющая собой квантовый процессор, должна содержать достаточно большое число N > 100 хорошо различаемых кубитов для выполнения соответствующих квантовых операций.

· Необходимо обеспечить условие для приготовления входного регистра в исходном основном базисном состоянии. То есть должна существовать достаточно легко реализуемая возможность инициализации (зануления) регистра и перевода кубитов в чистое состояние. Точнее, в псевдочистое, поскольку, как нам уже известно, никто пока не знает, как реализовать чистое состояние. Вполне вероятно, что здесь работает гипотеза об определяющей роли градиента энергии, реализуемого в системе (более подробно об этом см. в главе 5). Кстати, частный случай этого общего принципа как раз и используется в настоящее время и считается пока наилучшим — это метод Кори (предложен в 1996–1997 годы). Другие его названия — метод пространственного усреднения и метод градиентного поля.

· Необходимо ограничить процесс декогеренции квантовых состояний, обусловленный взаимодействием системы кубитов с окружающей средой, что приводит к разрушению суперпозиций квантовых состояний и делает невозможным выполнение квантовых алгоритмов. Время декогеренции должно, по крайней мере, в 10⁴ раз превышать время выполнения основных квантовых операций (время такта). Для этого система кубитов должна достаточно слабо взаимодействовать с окружением.

· Необходимо обеспечить за время такта выполнение требуемой совокупности квантовых логических операций, определяющей унитарное преобразование. Дело в том, что любую математическую операцию, как арифметическую (сложение, вычитание, умножение, деление и т. д.), так и логическую («и», «или» и т. д.), можно свести к ограниченному числу логических операций. Из них основные всего лишь три: операция CNOT (контролируемое НЕ, Controlled NOT, аналог исключающего ИЛИ в классических компьютерах) — это двухкубитная операция, а также две однокубитные операции — операция НЕ и преобразование Адамара (см. предыдущую главу, выражение 3.13). Умея выполнять эти операции над кубитами, можно реализовать любую программу для квантового компьютера.

· Необходимо уметь воздействовать на каждый кубит по отдельности, а также иметь возможность измерить состояния квантовой системы на выходе, то есть при выводе результата. Одним словом, выбор физической основы квантового процессора должен быть согласован с достаточно простым устройством ввода-вывода информации.

В настоящее время ведутся работы над следующими основными вариантами физической основы (элементной базы) квантового процессора.

● Использование в качестве квантового процессора пробирки с органической жидкостью, где кубитами являются ядра отдельных атомов со спинами 1/2, связанные косвенными спин-спиновыми взаимодействиями. Органическая жидкость в пробирке ведет себя как одна молекула этого вещества, точнее, все молекулы ведут себя одинаково в тех взаимодействиях, которые нам необходимы. Таким образом появляется возможность применить к макроскопическим объемам жидкости отработанные методики и техники ядерного магнитного резонанса (ЯМР). Индивидуальное обращение к отдельным кубитам заменяется одновременным обращением к соответствующим кубитам одновременно во всех молекулах большого ансамбля. Логические операции над кубитами (с помощью радиочастотных импульсов) и вывод результата осуществляется стандартными методами ЯМР. Компьютер такого рода получил название ансамблевого (bulk-ensemble quantum computer) квантового компьютера. Он может работать и при комнатной температуре. Время декогеренции квантовых состояний ядерных спинов в жидкости достаточно велико и может составлять несколько секунд. Именно при использовании этой элементной базы в настоящее время достигнут самый значительный успех в практической реализации квантовых вычислений. Лидером здесь является группа Исаака Чуанга. В 1998 году впервые в мире ею создан 2-кубитный квантовый компьютер; в 1999 году — 3-кубитный, который с использованием алгоритма Гровера совершал поиск в базе данных; в 2000 году — 5-кубитный. Последнее достижение этой группы — 7-кубитный квантовый компьютер*. 7 кубитов оказалось достаточно, чтобы на практике осуществить реализацию квантового алгоритма П. Шора по разложению на простые множители числа 15, были получены 3 и 5.

 

* Vandersypen L. M. K., Steffen M., Breyta G., Yannoni C. S., Sherwood M. H., Chuang I. L. Nature 414, 883 (2001). Как выглядит такой компьютер можно посмотреть на сайте IBM Research: http://domino.research.ibm.com/comm/pr.nsf/pages/rsc.quantum.html.

 

На первый взгляд, достижения скромные, однако не стоит забывать, что N кубитов заменяет 2^N обычных битов, то есть зависимость здесь экспоненциальная — добавление одного кубита увеличивает возможности квантового компьютера в два раза. Если 7 кубитов — это всего лишь 128 классических битов, то, например, 30 кубитов — уже 10⁹ классических единиц информации, а 100 кубитов заменят 10³⁰ обычных битов — просто гигантское число. На сайте Los Alamos National Laboratory (LANL)* можно прочитать, что 30-кубитный квантовый компьютер был бы, по грубым прикидкам, эквивалентен обычному компьютеру, выполняющему 10 триллионов операций в секунду. Такое быстродействие сопоставимо с производительностью самых мощных суперкомпьютеров, состоящих из тысяч процессоров.

 

* http://www.lanl.gov/news/releases/archive/00-041.shtml.

 

Однако, несмотря на все преимущества квантового процессора в «пробирке», его потенциал практически исчерпан, поскольку измеряемый на выходе сигнал экспоненциально убывает с ростом числа кубитов. Оценки показывают, что предельным значением, когда еще можно что-то измерить, является 10–13 кубитов. Но, кроме этого технического, существуют и чисто физические ограничения. Дело в том, что косвенные спин-спиновые взаимодействия, необходимые для организации основных логических операций, сами по себе очень слабые. В результате время выполнения логических операций оказывается чрезвычайно большим, а создаваемый компьютер имеет небольшое быстродействие. В этом случае более перспективными оказываются твердотельные квантовые компьютеры на основе ЯМР, поскольку диполь-дипольные взаимодействия ядерных спинов в несколько тысяч раз превосходят косвенные спин-спиновые взаимодействия. Мы рассмотрим этот случай чуть ниже. А пока назовем другие экспериментальные реализации квантового компьютера.

 

● Использование в качестве кубитов уровней энергии ионов, захваченных ионными ловушками, создаваемыми в вакууме определенной конфигурацией электрического поля в условиях их лазерного охлаждения до микрокельвиновых температур. Взаимодействие между заряженными ионами в одномерной цепочке этих ловушек осуществляется посредством возбуждения их коллективного движения, а индивидуальное управление ими — с помощью лазеров инфракрасного диапазона. Первый прототип квантового компьютера, соответствующий этим принципам, был предложен австрийскими физиками И. Цираком и П. Цоллером в 1995 году. В настоящее время интенсивные экспериментальные работы ведутся в LANL и в Национальном Институте стандартов и технологии (National Institute of Standards and Technology — NIST) в США. Преимущество такого подхода заключается в сравнительно простом индивидуальном управлении отдельными кубитами. Основными же недостатками этого типа квантовых компьютеров являются необходимость создания сверхнизких температур, обеспечение устойчивости состояний ионов в цепочке, а также ограниченность возможного числа кубитов значением N < 40. На сегодняшний день установлен практически полный контроль над квантовым состоянием единичного иона в ловушке, и внимание экспериментаторов переключилось на системы из нескольких ионов с хорошо контролируемыми взаимодействиями между ними. Действие квантовых логических схем основано в данном случае на квантовой запутанности внутренних степеней свободы ионов (электронные возбуждения) и коллективного движения (колебательного возбуждения) запертых в ловушке ионов.

 

● Использование в качестве кубитов зарядовых состояний куперовских пар в квантовых точках*, связанных переходами Джозефсона, предложенное Д. В. Авериным в 1998 году. Первый твердотельный кубит на основе этих принципов был создан в NEC Fund. Res. Lab. в Японии в 1999 году. Предполагается, что перспективность этого направления заключается в возможности создавать электронные квантовые устройства высокой степени интеграции на одном кристалле, при этом для управления кубитами не потребуются громоздкие лазерные или ЯМР-установки. Однако создание квантовых компьютеров по-прежнему сопряжено со многими трудностями — не решенным остается ряд важных проблем, в частности, устойчивости состояний кубитов и декогеренции.

 

* Что такое «квантовые точки», можно прочитать на сайте Scientific.ru: http://www.scientific.ru/journal/news/0203/n120203.html.

 

● В 2002 году появилось сообщение*, что исследователи из Висконсинского Университета в Мадисоне создали первую в мире симуляцию архитектуры квантового компьютера, применив кремниевую технологию изготовления. Эта архитектура, в которой используется горизонтальное и вертикальное туннелирование через двойные верхние и нижние ворота, занимает на чипе 50 кв. нанометров. Группа исследователей пришла к выводу, что современное оборудование для кремниевого производства пригодно и для производства квантовых чипов, хотя они пока работают со скоростью 1 МГц из-за больших требований к импульсному генератору. В качестве квантового бита были выбраны направления спина электрона 1 — вверх, 0 — вниз. В ходе эксперимента проведены простейшие вычисления, для чего было объединено несколько квантовых точек. Однако для того, чтобы производить действительно «полезные» вычисления, в компьютер понадобится добавить еще около 1 миллиона квантовых точек.

 

* http://www.cnews.ru/newtop/index.shtml?2002/08/07/134303.

 

Подробное описание (со схемами, рисунками и пояснениями) некоторых наиболее ярких экспериментальных работ, опубликованных в Nature и других ведущих журналах, можно прочитать на русском языке на сайте Scientific.ru:

Schrader D., Dotsenko I., Khudaverdyan M., Miroshnichenko Y., Rauschenbeutel A., and Meschede D., Phys. Rev. Lett. 93, 150501 (2004), http://www.scientific.ru/journal/news/1004/n211004.html;

Achermann M., Petruska M. A., Kos S., Smith D. L., Koleske D. D., Klimov V. I., Nature 429, 642 (2004), http://www.scientific.ru/journal/news/0804/n260804.html;

Elzerman J. M., Hanson R., Willems van Beveren L. H., Witkamp B., Vandersypen L. M. K., Kouwenhoven L. P., Nature, 431, 431 (2004), http://www.scientific.ru/journal/news/0904/n030904.html.

 

В начале 2005 года в журнале «Успехи физических наук» (УФН) была опубликована большая обзорная статья академика К. А. Валиева «Квантовые компьютеры и квантовые вычисления», УФН 175 (1), 3 (2005), в которой упоминаются следующие основные направления реализации квантовых вычислений (помимо ЯМР):

 

1. На ионах в одномерном ионном кристалле в ловушке Пауля.

2. В полупроводниковых кристаллах бесспинового моноизотопного кристалла кремния ²⁸Si, в котором атомы фосфора ³¹Р (кубиты) расположены в линейной цепочке (модель Кейна). Темп развития этого направления, признаваемого всеми весьма перспективным, определяется темпом нанотехнологических разработок, необходимых для создания структур с нужными параметрами.

3. Кубиты на электронах в полупроводниковых квантовых точках. В качестве кубитов исследуются орбитальные или спиновые состояния одиночного электрона в квантовой точке.

4. Кубиты на сверхпроводниковых мезоструктурах. Здесь существуют два варианта: в первом — квантовая информация кодируется числом сверхпроводящих пар в квантовой точке, во втором — направлением сверхпроводящего тока в сквиде.

5. На одиночных атомах в микрорезонаторах. Двухуровневая система (атом-кубит), связанная с осциллятором-фотоном в одной из мод колебаний резонатора. Этот метод предполагается использовать при разработке способов транспортировки атомных и фотонных кубитов, а также при передаче квантовой информации от атомных кубитов к фотонным и обратно (атом-фотонный квантовый интерфейс).

6. С помощью линейных оптических элементов (оптический квантовый компьютер).

 

Все эти методы в той или иной мере уже реализованы экспериментально.

 

Есть также ряд перспективных идей:

1. Двумерный электронный кристалл в потенциальной ловушке (яме) вблизи поверхности жидкого гелия.

2. Двумерная решетка атомов в оптической ловушке, образованной стоячей волной интерферирующих лазерных пучков.

3. Анионы в двумерном электронном газе в полупроводниках в условиях дробного квантового эффекта Холла.

4. Квантовые клеточные автоматы в ферромагнитных (антиферромагнитных) структурах в кристаллах.

 

К наиболее существенным достижениям последнего времени можно отнести результаты двух экспериментальных работ в этой области, одновременно опубликованные в Nature (1 декабря 2005 года)*. Двум конкурирующим командам физиков из США и Австрии почти одновременно удалось запутать рекордное число индивидуальных частиц. Дитрих Лейбфрид с коллегами из NIST в Колорадо запутали 6 ионов бериллия, в то время как Гартмут Хеффнер с сотрудниками из университета Инсбрука — 8 ионов кальция.

 

* Leibfried D. et al., Creation of a six-atom “Schrodinger cat” state, Nature 438, 639–642 (2005); Häffner H. et al., Scalable multiparticle entanglement of trapped ions, Nature 438, 643–646 (2005).

 

В первой статье сообщается о реализации cat-состояния четырех-, пяти- и шестиатомных кубитов. Пространство состояний каждого кубита определено двумя сверхтонкими основными состояниями иона бериллия. Cat-состояние соответствует запутанной равновесной суперпозиции всех атомов в одном сверхтонком состоянии и одновременно всех атомов в другом сверхтонком состоянии. Это состояние типа 1/√2(|000000ñ + |111111ñ). Для наглядности это можно представить так, что все ионы вращаются одновременно и по часовой стрелке, и против нее. В этих экспериментах cat-состояния приготавливались в процессе трех последовательных шагов независимо от числа запутанных атомов.

Во второй статье речь идет об экспериментальной реализации четырех-, пяти-, шести-, семи- и восьми запутанных частиц в состояния типа W в ионных ловушках. Авторы демонстрируют, как получить максимально возможную информацию об этих состояниях, выполняя полное определение параметров посредством так называемой томографии состояния*, используя индивидуальный контроль и детектирование ионов. Детальный анализ подтверждает, что запутанность является подлинной. Возможность приготовления таких многочастичных запутанных состояний вместе с полной информацией в форме матрицы плотности создает испытательный полигон для более глубоких теоретических исследований многочастичной запутанности.

 

* См., например, White A. G., James D. F. V., Eberhard Ph. H. and Kwiat P. G. Phys. Rev. Lett. 83, 3103 (1999); James D. F. V., Kwiat P. G., Munro W. J. and White A. G. Phys. Rev. A 64, 052312 (2001), в свободном доступе: http://arxiv.org/abs/quant-ph/0103121; Thew R. T., Nemoto K., White A. G., Munro W. J. Phys. Rev. A 66, 012303 (2002), в свободном доступе: http://arxiv.org/abs/quant-ph/0201052.

 

Интересно, что в обеих статьях речь идет о реализации двух различных типов максимально запутанного состояния. Если в первой говорится о cat-состояниях, частным случаем которых являются хорошо известные ГХЦ-состояния (GHZ — Greenberger-Horne-Zeilinger*) для трех частиц, то во второй работе — о так называемых W-состояниях. Это суперпозиционное состояние типа |00...01ñ + |00...10ñ + ... + |01...00ñ + |10...00ñ с равными весами, то есть когда есть одна единичка, а все остальные — нули, либо симметричное ему состояние: один нуль, остальные — единички. Мне встречалась версия, согласно которой свое название «W-состояния» они получили по имени Wolfgang (W. Dür), это обозначение было введено в статье**.

 

* Greenberger D. M., Horne M. A., and Zeilinger A., in Bell’s Theorem, Quantum Theory, and Conceptions of the Universe, edited by M. Kafatos (Kluwer, Dordrecht, 1989). Р. 69.

** Dür W., Vidal G. and Cirac J. I. Phys. Rev. A 62, 062314, (2000).

 

Состояния cat- и W-типа являются основными классами состояний, на которых отрабатываются теоретические методы анализа квантовой запутанности. Их характеристики хорошо изучены, и основное различие между ними состоит в том, что cat-состояния более чувствительны к таким внешним манипуляциям, как измерение. Например, в случае ГХЦ-состояния (трехчастичное cat-состояние), если удалить любую из трех подсистем, то оставшиеся две будут не запутаны, классически коррелированны. Другими словами, парные корреляции — классические, но в то же время корреляции одной частицы с двумя другими — чисто квантовые, и, как целое, это состояние максимально запутанное. Таким образом, cat-состояние (произвольной размерности) служит примером максимально запутанного, когда вся большая система находится в нелокальном состоянии, но на уровне подсистем (в пространствах состояний меньшей размерности) существуют локальные объекты. Шредингеровские коты вовсе не обязаны быть на уровне подсистем, там можно найти и вполне обычных «котов», несмотря на то что исходная система, «самый большой кот» — шредингеровский. 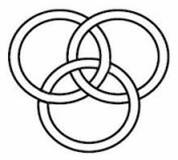Глядя «изнутри» cat-состояния, когда одна подсистема «смотрит» на своих соседей, она будет видеть каждого из них по отдельности в виде локальных объектов.

Когерентность на уровне замкнутой системы вовсе не означает полную когерентность на уровне подсистем — там могут быть самые различные ситуации, в том числе сепарабельные состояния в различных сочетаниях.

Другой класс — W-состояния, основная особенность которых в том, что при удалении одной частицы запутанность между другими сохраняется, не разрушается. В этом их отличие от cat-состояний.

Таким образом, экспериментаторы научились не просто приготавливать многочастичные запутанные состояния, но и реализовать тот или иной тип запутанности в системе. Различные классы запутанных состояний предполагается использовать в зависимости от их особенностей. Авторы первой статьи, сумевшие получить 6-частичное cat-состояние, говорят о том, что их метод можно использовать, например, в квантовой криптографии, где нужна большая чувствительность — при попытке «подслушать» квантовый канал связи запутанность должна тут же разрушаться. Авторы второй статьи, реализовавшие 8-частичное W-состояние, предполагают, что состояния такого типа больше подходят для квантовых вычислений.

А теперь в качестве небольшого отступления рассмотрим известную топологическую структуру, которая называется «кольца Борромео», что поможет вам более наглядно представить, что такое ГХЦ-состояние. Это три кольца (рис. 4), попарно не сцепленные, но в совокупной целостности разъединить их не удается. Кольца соединены таким способом, при котором любые два кольца скрепляются посредством третьего. Такие кольца были изображены на фамильном гербе знаменитого в эпоху Возрождения итальянского семейства Борромео, откуда они и получили свое название.

 

Рис. 4. Кольца Борромео

 

Если подразумевать под кольцами физические подсистемы, то их характерной особенностью является то, что если одно кольцо убрать, то два оставшихся не будут связаны квантовыми корреляциями. Они станут сепарабельными (разделимыми), то есть их запутанность распадается с удалением любого кольца. В этом — их полная аналогия с ГХЦ-состояниями. Эта особенность была замечена практически сразу, как только были проанализированы запутанные состояний ГХЦ-типа, и П. К. Аравинд инициализировал новое направление по изучению топологии запутанности, опубликовав в 1997 году статью «Борромео запутанность ГХЦ-состояний»*. Данное направление сейчас активно развивается, что подтверждается некоторыми интересными публикациями**.

 

* Aravind P. K., Borromean entanglement of the GHZ state, Quantum Potentiality, Entanglement and Passion-at-a-Distance: Essays for Abner Shimony, eds. R. S. Cohen, M. Horne and J. Stachel, Kluwer, Dordrecht, 1997. Р. 53–59.

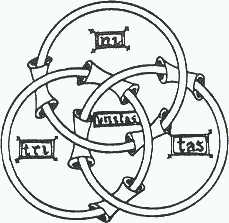
** Kauffman L. H. and Lomonaco S. J. Quantum entanglement and topological entanglement, New J. Physics 4. Р. 73.1–73.18 (2002).

 

Кольца Борромео как топологическая структура используются в качестве символа христианской Троицы. Ранее нередко встречались такие символы, как равносторонний треугольник, круг и некоторые другие, но сейчас все чаще Троицу изображают в виде колец Борромео. Одним из самых ранних источников, где было приведено такое символическое изображение Пресвятой Троицы, считается рукопись тринадцатого столетия, которая хранилась в муниципальной библиотеке г. Шартр (Chartres) во Франции. К сожалению, рукопись погибла в огне в 1944 году. Копия рисунка из этой рукописи (рис. 5.) воспроизведена из «Христианской иконографии»* наряду с описанием трех других диаграмм (рис. 6).

 

* Didron M. and Didron A. N., Christian Iconography, or the History of Christian Art in the Middle Ages, George Bell and Sons, London, 1886. Источник: http://www.liv.ac.uk/~spmr02/rings/trinity.html.

 

 

Рис. 5. Символическое изображение Пресвятой Троицы. Надпись в центре «unitas» — один (единение, единство). Три слога «tri-ni-tas» — три (трое), распределены во внешних секторах

 

 

Рис. 6. Другие варианты надписей:

а) Бог есть Жизнь (Vita Deus), окруженная Отцом (Pater), Сыном (Filius) и Духом Святым (Spiritus Sanctus);

б) Deus Est — Бог есть, является: Словом (Verbum), Светом (Lux) и Жизнью (Vita);

в) на последней диаграмме фразы: «Trinitas Unitate» (Три в Одном) и «Unitas Trinitate» (Один в Трех)

 

Ближе к магии древний скандинавский символ, который имеет точно такую же топологию, как и кольца Борромео, — это треугольники Одина (рис. 7.).

 

 

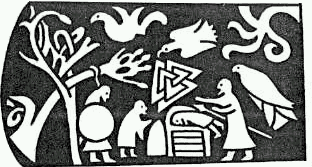
Рис. 7. Треугольники Одина (Валькнут)

 

В рунической магии он называется Валькнут. Переплетение трех треугольников ГХЦ-типа — это символ Одина и связанной с ним магии, символ переходов (мостов) между мирами. Валькнут часто встречается при археологических раскопках на древних рунических камнях (как правило, поминальных) рядом с изображениями Одина или павших воинов (рис. 8.). Его иногда так и называют — Узел Павших или Узел Избранных. Три переплетенных треугольника символизируют три мира: мир богов (Асгард), мир людей (Мидгард) и мир мертвых (Хель). Как говорит А. Платов*: «Три мира переплетены в этом символе Отца Магии; следует видеть в этом знак того, что маг черпает Силу и мудрость изо всех трех миров, взаимопроникающих и пересекающихся чаще, чем об этом думают. Валькнут — своего рода Северная Мандала... Созерцание такого глубокого магического символа, как Валькнут, и размышление о его сути — возможно, это одна из тех многих тропок, что могут вести к самотрансформации...»

 

* Платов А., Дарт А. ван. Практический курс рунического искусства. К.: София, 2000.

 

 

Рис. 8. Изображение Валькнута на одном из скандинавских поминальных камней (рис. с сайта http://www.liv.ac.uk/~spmr02/rings/vikings.html).

 

Как нам уже известно, описание в терминах вектора состояния — полное, поэтому можно утверждать, что модель трехкубитной Вселенной способна полностью описать (количественно!) руническую магию Одина. Чтобы получить что-то новое, мы можем расширять модель, рассматривать четырех-, пяти- и т. д. кубитные модели. Если не просто созерцать этот «глубокий магический символ» и размышлять о его сути, как пишет А. Платов, но еще и уметь количественно его описывать, то это будет не просто путь к самотрансформации, а нечто несоизмеримо большее.

В рунической магии пытаются использовать некий примитивный аналог количественного описания. Рассматривают 8 положений Валькнута (замечу, что для трехсоставной системы полный базис состоит как раз из 8 собственных состояний — 2³ = 8), круг из 24 рун — и каждому положению Валькнута соответствует свой набор рун, управляющих перераспределением энергии между мирами (градиентами энергии). По сравнению с этим, количественное описание в трехкубитной модели будет полным, охватывающим все ситуации, хотя какие-то подсказки из рунической магии или сопоставления с ней здесь могут быть интересны.

Руны, расположенные по кругу, образуют рунический круг, и, согласно древней скандинавской традиции, эволюция Мира происходит циклически. Исходной является руна Феху как предшественница всего тварного (нелокальный источник реальности), как творческий замысел, содержащий опыт (квантовую информацию), накопленный в предыдущих циклах. Далее идет руна Уруз как сила (градиент энергии), способная воплотить замысел и оформить его в виде локальных структур. Следующая Турисаз — руна, организующая и направляющая слепую «силу быка» предыдущей руны в нужное русло... и т. д. по руническому кругу до Дагаз. Руна Дагаз — плодотворное завершение тварного периода существования локальных форм с сохранением опыта для последующих циклов. После этого снова следует руна Феху как конец и начало следующего периода. Считается, что такие рунические циклы характерны как для глобальных процессов во Вселенной, так и для незначительных локальных. Обычно руне Феху ставят в соответствие 1-ю и 64-ю гексаграммы из «Книги Перемен», другим рунам тоже соответствуют свои гексаграммы. Замечу, что описание в терминах гексаграмм ближе к квантовомеханическому описанию, поскольку матрица плотности трехсоставной системы содержит как раз 64 элемента — столько же, сколько гексаграмм.

Заметны параллели и с другими традициями, в частности, с восточными (см. об Инь/Ян в предыдущей главе), которые аналогично описывают эволюцию Вселенной. И здесь опять динамику Универсума можно свести к однокубитной модели, поскольку ГХЦ-состояния (треугольники Одина) и их обобщение — cat-состояния произвольной размерности, имеют всего два основных базисных состояния и описываются эволюцией однокубитного вектора состояния при его движении по сфере Блоха.

Я просмотрел в Интернете несколько русскоязычных ресурсов по рунам, и меня несколько удивило то обстоятельство, что все, кто занимается рунической магией, не видят главной топологической особенности Валькнута, этого основного символа Одина — скандинавского «отца магии». Упоминание о треугольниках Одина, как о примере ГХЦ-состояний (наряду с кольцами Борромео), я прочитал в физической статье. Именно физики обращают внимание магов на их основополагающие символы и поясняют, в чем заключается их основная «сила» — в суперпозиционных состояниях и нелокальных квантовых корреляциях.

Никто из рунических магов почему-то не комментирует и не обсуждает особый вид переплетения треугольников на изображении Валькнута. Треугольники попарно не сцеплены, не соединены, как, например, мир богов и наш срединный мир, но тем не менее расцепить их невозможно — они составляют единое целое. Это означает, что все связи между тремя мирами осуществляются не через некие мифические, непонятные «перемычки» или «мосты», а только посредством нелокальных квантовых корреляций. И эти нелокальные корреляции легко объясняются и описываются на простых моделях в квантовой теории. Думаю, последователи рунической магии открыли бы для себя много новых удивительных практик, если бы немного познакомились с физикой квантовой информации. Впрочем, это относится и ко всем другим «магиям» и эзотерическим практикам. Все последствия перехода от мифов и сказок к количественному описанию магических практик я не могу себе представить. Могу только сказать, что эти последствия будут очень значительными, может быть, просто катастрофическими, а может, наоборот, спасительными...

Однако пора уже вернуться «к нашим баранам» и продолжить разговор о физической реализации запутанных состояний.

В середине 2005 года в журнале «Physical Review Letters» была опубликована статья об экспериментальной реализации многофотонной запутанности оптическими методами*.

 

* O’Sullivan-Hale M. N., Ali Khan I., Boyd R. W. and Howell J. C. Phys. Rev. Lett. 94 220501 (2005).

 

Сотрудники Университета Рочестера (США) продемонстрировали простой экспериментальный метод создания запутанных кубитов. Используя поперечный импульс и запутанность положения фотонов, испускаемых в процессе спонтанного параметрического преобразования (частоты) вниз (SPDC — spontaneous parametric down-conversion)*, авторы получили запутанность между дискретными областями пространства, то есть пикселями. Каждый фотон отображался на 6 пикселей — каждый пиксель представлял один уровень состояния кубита. Этот метод легко обобщить для создания запутанных состояний более высокой размерности. Таким образом, возможна реализация процесса квантовой обработки информации в системах произвольно высокой размерности.

 

* В русскоязычной литературе этот процесс известен под названием «спонтанное параметрическое рассеяние (СПР) света». См., например: Клышко Д. Н. Фотоны и нелинейная оптика. М: Наука, 1980. Применительно к запутанным состояниям см.: Бауместер Д., Экерт А., Цайлингер А. Физика квантовой информации. М.: Постмаркет, 2002. С. 80.

 

В этом эксперименте ультрафиолетовый лазерный луч направлялся на кристалл с нелинейными оптическими свойствами (β-борат бария), который спонтанно расщепляет ультрафиолетовый фотон на пару запутанных инфракрасных фотонов. Рочестерская команда фактически запутывает импульсы фотонов, это означает, что их положения в реальном месте (координаты), как показывает детектор, также запутаны.

Эти исследования демонстрируют, что фотоны могут занять любой из шести импульсов или пикселей (положений состояния). Хотя запутанные кубиты к настоящему времени получают самыми различными способами, авторы утверждают, что их метод привлекателен из-за сравнительной простоты в реализации. Как сказал руководитель группы сотрудникам редакции «PhysicsWeb»*: «Мы работаем с простой, имеющейся в наличии оптикой, без потребности в голограммах или интерференционной стабильности, как в предыдущих экспериментах». Теперь команда планирует продемонстрировать запутанность пикселей в квантово-криптографических системах. «Мы также хотели бы использовать наши идеи, чтобы создать высокоразмерные запутанные состояния, используя другие переменные, типа энергии и времени», — добавляет О’Салливан-Хэйл.

 

* http://physicsweb.org/articles/news/9/6/11.

 

Лабораторные эксперименты в области квантового компьютинга все ближе подходят к реальным технологиям. Группа исследователей компании Хитачи, работающая в Кембриджском университете в Великобритании, в августе 2005 года сообщила* о разработке кремниевого кубитного чипа — первом шаге в развитии квантового компьютера, основанного на обычной кремниевой технологии.

 

* Сообщение на сайте Хитачи: http://www.hitachi.com/New/cnews/050819.html, опубликовано: Gorman J., Hasko D. G. and Williams D. A. Phys. Rev. Lett. 95, 090502 (2005).

 

Ранее кубиты уже создавались на основе арсенида галлия, но время декогеренции, в течение которого сохраняется когерентность состояния кубита, было очень малым. Ученые компании Хитачи продемонстрировали, что изолированная двойная квантовая точка (наноскопическая пространственная неоднородность), созданная на кремниевом кристалле, проявляет себя как кубит со временем декогеренции, в 100 раз большим, чем предыдущая реализация в арсениде галлия. Методика создания квантовых точек уже отработана и может быть использована в стандартных КМОП-процессах (CMOS, complimentary metal oxide semiconductor — полупроводниковая технология, применяемая при изготовлении всех логических микросхем, включая микропроцессоры и чипсеты). Одного лишь создания кубита для построения квантового компьютера недостаточно, и кембриджская команда Хитачи произвела все базовые операции: инициализации; манипуляции — с помощью электронных гейтов; измерения — с использованием одноэлектронных транзисторов. Предложенная схема обладает гибкостью, так как кубиты могут быть объединены в разнообразные двумерные цепи, как в обычных микропроцессорах. Это дает возможность наращивать число кубитов до большой квантовой схемы, что необходимо для создания полноценного квантового компьютера.

В начале 2006 года ученые из Университета Мичигана (США) сообщили* о том, что для создания кубита им удалось воспользоваться технологией MEMS, которая сейчас все шире применяется в промышленном производстве.

 

* Stick D., Hensinger W. K., Olmschenk S., Madsen M. J., Schwab K. and Monroe C. Ion trap in a semiconductor chip, Nature Physics 2, 36 (2006).

 

Технология MEMS (Micro-Electro-Mechanical-System) позволяет формировать на поверхности подложки микроэлектромеханические структуры различного функционального назначения. По этой технологии изготавливаются интегральные акселерометры (датчики ускорения), микромоторы, селективные фильтры для биотехнологий и модуляторы света. Микроэлектромеханические системы создаются посредством комбинирования механических элементов, датчиков и электроники на общей кремниевой основе с использованием технологий микропроизводства. Все элементы могут быть реализованы в виде единого изделия — микросхемы на кремниевой пластине, причем выпускать их можно сразу десятками или сотнями. При этом в основе лежит уже апробированная традиционная технология производства полупроводниковых интегральных микросхем.

В MEMS используют обычно два различных вида микрообработки: объемную и поверхностную. Объемная микрообработка включает технологию глубинного объемного травления. При использовании такого процесса объемная структура получается внутри подложки благодаря ее анизотропным свойствам, то есть различной скорости травления кристалла в зависимости от направления кристаллографических осей. Объемная структура может наращиваться, что и происходит, когда несколько подложек сплавляются и образуют вертикальные связи на атомарном уровне. При поверхностной микромеханической обработке трехмерная структура создается последовательным наложением основных тонких пленок и удалением вспомогательных слоев согласно требуемой топологии. Преимущество данной технологии заключается в возможности многократного удаления (растворения) вспомогательных слоев без повреждения взаимосвязей базовых слоев. Ее главная особенность в том, что она совместима с полупроводниковой технологией, поскольку для микрообработки используется обычный КМОП-процесс.

Так вот, ученые из Мичигана продемонстрировали, что ионные ловушки, которые сейчас широко используются в квантовом копьютинге, можно создавать не вручную, а с использованием промышленной MEMS-технологии. Они создали ионную ловушку из четырех последовательных слоев алюмогаллиевого арсенида на подложке из арсенида галлия, используя молекулярно-лучевую эпитаксию. Ученые проделали отверстие в чипе и сформировали ряд консольных электродов с помощью методов, обычно применяемых при изготовлении микроэлектромеханических систем (MEMS). Они установили чип в вакуумное гнездо и через отверстие ввели газ атомов кадмия, используя импульсный лазер. Тщательно регулируя такие параметры, как напряжение электрода и длина волны лазера, ученые смогли получить в ловушке единственный ион ¹¹¹Cd⁺ и научились управлять его квантовым состоянием. Авторы сообщают, что такие ловушки обладают высокой надежностью и обеспечивают высокий уровень контроля и манипулирования отдельными состояниями. Как они пишут, метод «предоставляет беспрецедентный контроль на уровне единственного атома». В качестве примера практического применения упоминаются прежде всего крупномасштабные квантовые процессоры, поскольку с помощью этого метода можно изготавливать большое количество кубитов.

Таким образом, научные исследования в сфере разработки квантового процессора уже вплотную подошли к промышленным технологиям.

К числу интересных, но пока нереализованных идей можно отнести предложение применять для квантовых вычислений так называемые квантовые проволоки и новейшие достижения спинтроники. Еще несколько лет назад ученые из Кембриджского университета предложили использовать распространение электронных волн по квантовым нитям для проведения квантовых вычислений. Для создания кубита использовали управляемое туннелирование волн из одного канала в другой, а для организации двухкубитных операций — кулоновское взаимодействие электронов, находящихся в соседних каналах. Сейчас предлагается* распространить эту идею на спины, поскольку время декогеренции спиновых степеней свободы гораздо выше. За это время электрон пролетает большие расстояния, а значит, сама структура будет крупнее и, следовательно, проще в изготовлении. Для осуществления универсальных квантовых гейтов (логических операций) здесь можно использовать обменное и спин-орбитальное взаимодействие кубитов. Инициализация и измерение могут быть выполнены любой спиновой инжекцией из/в ферромагнетиков (и) или с использованием спиновых фильтров и мезоскопических спин-поляризующих светоделителей. Авторы (A. E. Popescu, R. Ionicioiu) также оценивают пригодность различных материалов, используемых в настоящее время в нанотехнологиях, для физической реализации своей модели.

 

* Popescu A. E. and Ionicioiu R. Phys. Rev. B 69, 245422 (2004).

 

Существует и много других интересных предложений, которые пока не реализованы. Одно из них мы рассмотрим подробнее, поскольку чуть далее я укажу на интригующую связь этого варианта реализации квантового компьютера с эзотерикой, точнее, с возможной локализацией квантового компьютера в нашем головном мозге.

Речь идет о твердотельном квантовом компьютере, где в качестве квантового процессора используются кристаллы гидроксиапатита кальция Ca₅(PO₄)₃OH, или его аналоги (фторапатит и др.). Эти монокристаллы считаются очень перспективными кандидатами* на роль физической основы твердотельного квантового компьютера, который можно реализовать методами ЯМР.

 

* Ladd T. D., Goldman J. R., Dana A., Yamaguchi F. and Yamamoto Y. arXive e-print quant-ph/0009122, (2001), http://xxx.itep.ru/abs/quant-ph/0009122.

 

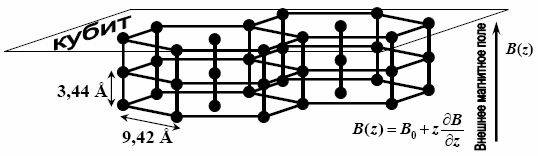
Природа, словно по заказу, создала материал, идеально подходящий для реализации квантового компьютера. Микроструктура кристалла представляет собой плоскости, перпендикулярные одномерным цепочкам протонов гидроксильных групп. Каждая цепочка окружена 6 аналогичными, и существенно то, что расстояние между отдельными «нитями» почти в три раза больше, чем расстояние между протонами в самой цепочке (рис. 9). Поскольку диполь-дипольное взаимодействие (ДДВ) ядерных спинов убывает с расстоянием как 1/r³, константа ДДВ между ближайшими ядрами в одной цепочке в десятки раз больше максимальной константы ДДВ спинов в соседних «нитях». Поэтому можно считать, что отдельные цепочки ядерных спинов слабо взаимодействуют между собой. В некотором приближении можно рассматривать структуру гидроксиапатита как квазиодномерную (линейную). Это позволяет оперировать целыми плоскостями протонов так, как будто это одиночные линейно расположенные ядерные спины.

В одной из статей* предлагается создать твердотельный квантовый компьютер методами ЯМР на монокристалле гидроксиапатита кальция, помещенном в сильное магнитное поле, изменяющееся вдоль одной из осей монокристалла. В таком компьютере можно организовать согласованную работу очень большого числа кубитов.

 

* Fel’dman E. B., Lacelle S. Perspectives on a Solid State NMR Quantum Computer, arXiv.org:quant-ph/0108106, (2001); http://xxx.itep.ru/abs/quant-ph/0108106.

 

 

Рис. 9. Кристаллическая структура гидроксиапатита кальция. Черными точками обозначено расположение протонов. Кубитами являются плоскости монокристалла, состоящие из протонов, перпендикулярные внешнему магнитному полю.

 

Основные идеи, предложенные Э. Б. Фельдманом и С. Ласеллем, следующие:

1. Каждая плоскость монокристалла, перпендикулярная магнитному полю, является кубитом. Представление о количестве таких плоскостей дает тот факт, что кристалл гидроксиапатита кальция размером 3,5×9,5×9,5 см содержит 10⁸ плоскостей, каждая из которых имеет 10¹⁶ протонных ядерных спинов.

2. ДДВ ядерных спинов усредняются методами Ли-Гольдбурга. При этом ДДВ двух выбранных плоскостей (двух кубитов) восстанавливаются с помощью дополнительного селективного облучения монокристалла двумя высокочастотными (ВЧ) полями, перпендикулярными так называемому «магическому» для ДДВ направлению. ДДВ ядерных спинов в выбранных плоскостях усредняются многоимпульсными последовательностями.

3. Однокубитные операции (логическое НЕ) выполняются с использованием π-импульсов ВЧ поля.

4. Двухкубитные операции (контролируемое НЕ) выполняются с использованием ДДВ кубитов.

 

К сожалению, с технической точки зрения реализация этого варианта квантового компьютера пока не осуществима, поскольку здесь нужно уметь создавать сильные градиенты магнитного поля порядка 10⁶ Гаусс/см. В настоящее время технически достижимые градиенты — порядка 10⁴ Гаусс/см. Однако принципиальных запретов на получение полей с большим градиентом не существует, есть только технические трудности, которые со временем могут быть преодолены.

Интерес к гидроксиапатиту кальция в качестве перспективной основы твердотельного квантового компьютера со стороны ЯМР-сообщества вовсе не случаен — он вызван подходящей структурой его кристаллической решетки. В этом как раз и заключается основная проблема — найти соединение с подходящей структурой, и если бы все было так просто, то твердотельный квантовый компьютер был бы уже реализован. Я говорю сейчас о реализации методами ЯМР — при использовании других методов, естественно, будут свои требования к физической основе квантового компьютера.

В случае с гидроксиапатитом существенно то, что монокристалл представляет собой параллельные плоскости, состоящие из протонов, и каждая такая плоскость может играть роль кубита. Таким образом, кубитом является не отдельный спин, а большое число ядерных спинов, лежащих в одной плоскости, и манипулировать ими становится гораздо легче, поскольку речь идет о макроскопических величинах. Другими словами — это вариант ансамблевого квантового компьютера, подобный тому, который реализован на сегодняшний день методами ЯМР в жидкостях. Проблема в том, что техническая реализация требует сильных градиентов внешнего магнитного поля, для того чтобы эти плоскости можно было отличать друг от друга и использовать для локальной адресации кубитов.

Не исключаю, что есть и другие кристаллы, которые, возможно, даже лучше подходят для этих целей. Я не специалист по кристаллам, и мне сложно судить об этом. В любом случае для этих целей хорошо бы иметь параллельные плоскости из ядер, обладающих магнитным моментом (протоны, фтор, фосфор, изотоп углерода ¹³C и т. д.). Считывание состояний этих плоскостей методами ЯМР не составляло бы проблем, если бы было приложено внешнее магнитное поле с достаточно сильным градиентом. Такой градиент позволил бы «раздвинуть» эти плоскости в частотном диапазоне, чтобы они не сливались, были индивидуально различимы и доступны для избирательного воздействия посредством селективных радиочастотных импульсов.